Meta-Learning without Memorization

Paper link: OpenReview.net
Code link: Google Research Github

Let’s consider how people learn as students. In the morning, we go to school, taking classes and answering questions asked by teachers. In the evening, we go back home, finishing homeworks and checking the answer keys. This daily routine can be considered as solving a task everyday, with task training in class and validation at home. In the end, when graduate from school, we not only obtain specific knowledge, but learn how to learn. Meta-learning is a paradigm in artificial intelligence that mimics such learning procedure. By leveraging experience from previous tasks, the algorithm aims to be able to solve a new task by fast adapting to a few training data. However, to develop the adapting ability, the learner has to avoid a problematic approach which we refer to as the memorization in meta-learning.

TL;DR: In this paper, we aim to answer the main questions: What is the memorization problem in meta-learning? Why does the memorization problem happen? How can we prevent it?

Basics

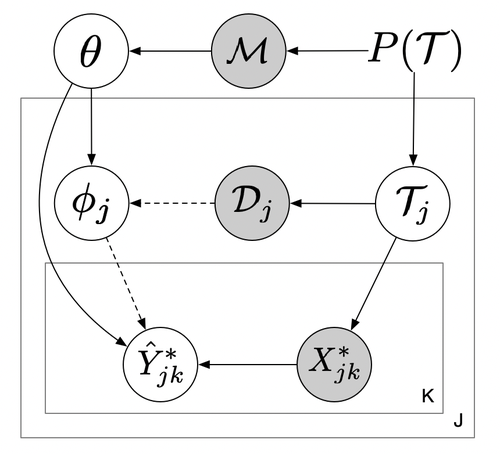
To set things up, assume there are multiple tasks generated from a task distribution $p(\mathcal{T})$. Each task has some labeled training data $\mathcal{D} = (X,Y)$ and test data $\mathcal{D}^{\star} = (X^{\star},Y^{\star})$. $\mathcal{M}$ represents all the meta-training data and $\mathcal{T}_j$ is a new task. The meta-learner is trained on $\mathcal{M}$, adapted on the new task training data $\mathcal{D}_{j},$ and aims to make good predictions on the new task test inputs $X^{\star}_{j}$. This process can be summarized in a hierarchical graphical model:

Memorization Problem

Let’s come back to the student example at the beginning. The daily study at school can be considered as a task in meta-training, and we assume the student learns to solve one type of math problem every day. After a period, assume all types of required problems have been reviewed several times in class $($like what we once did for an important exam 💆$)$. If a student can remember all problem types, he/she can answer the homework questions of these problem types correctly, without attending the class. Though such seemingly innocuous memorization approach can solve new problems of the known types, however, when the student faces an unseen type of problem, he/she cannot solve it merely based on the memorized knowledge, without learning from new resources.

Let’s consider another illustrative example. Assume each task is a 1D regression on some related data. In the following figures, a meta-learning algorithm is trained to adapt on a few training data, as the red points, and to fit on the validation data, as the blue points, where the dashed line represents a good adapted model

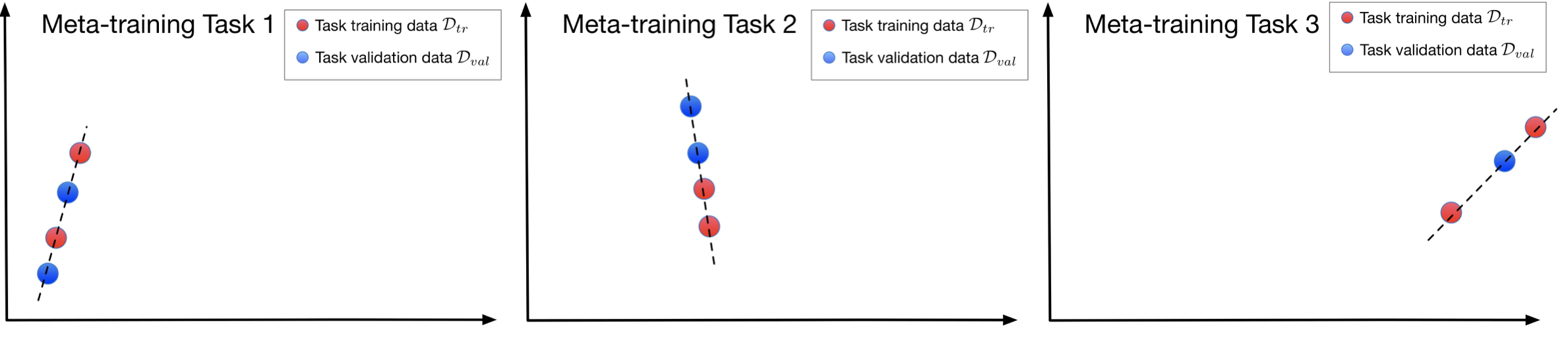
By training on multiple correlated tasks, the model develops a fast adaptation ability, which can generalize to solving tasks that are unseen in the meta-training, as the left figure below. However, we find if the meta-learner is flexible enough, a single model can solve all the training tasks without adapting to the task training data, as the right figure below. In the test-time, when facing a new task, the algorithm will not know how to utilize a few task training data to infer the local parameters and therefore cannot solve the new task.

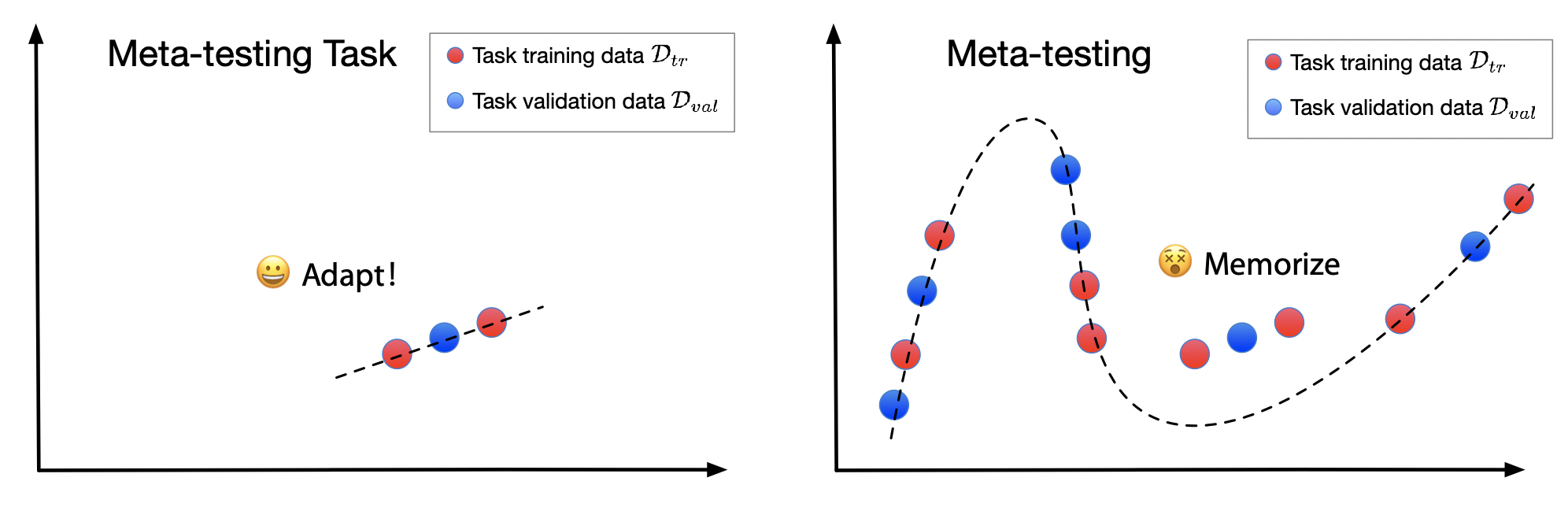
We call this phenomenon as the $($complete$)$ memorization problem in meta-learning. We formally define it as

\begin{equation} I(\hat{y}^{\star};\mathcal{D} | x^{\star}, \mathcal{M})=0 \end{equation}

which means the predicted label and the task training data are conditionally independent.

Notice the memorization problem is closely related to the task distribution. We find that if the meta-training tasks are mutually exclusive, which means a single model cannot solve all the tasks, the memorization problem will not happen. For example, in the few-shot classification problems, mutually exclusive tasks are created by randomly shuffling the labels across tasks. However, in a wide range of problems the tasks are non-mutually exclusive. Therefore, the memorization problem widely exists and can influence a variety of meta-learning algorithms.

Meta-Regularization

Based on the above analysis and the graphical model, we find that the information that is used to predict the task test labels comes from the meta-traing data $\mathcal{M}$, task training data $\mathcal{D}$ and task test input $x^\star$. Hence, if we can limit the information that flows from $\mathcal{M}$ and $x^\star$, and in the meantime ask for accurate predictions, we can encourage the model to use the information in $\mathcal{D}$ rather than ignoring it. Using the inequalities in information and PAC-Bayes theory, one approach to the meta-regularization we derived is based on the information bottleneck, which regularizes

\begin{equation} D_{KL}(q(z^\star | x^\star, \theta)||r(z^\star )) \end{equation}

The other approach is to regularize

\begin{equation} D_{KL}(q(\theta | \mathcal{M})||r(\theta)) \end{equation}

where $\theta$ are the parameters of an encoder: $x \to z$. Notice we should only regularize the parameters that are not used in the adaptation, which differs from stardand regularizations. Combining the meta-regularization with the objectives in Model Agnostic Meta-Learning $($MAML$)$ and Conditional Neural Process $($CNP$)$, we name our proposed new algorithms as MR-MAML and MR-CNP. We apply them to several datasets where the tasks are non-mutually exclusive, where the standard meta-learning algorithms can fail. The algorithms are tested on a pose prediction dataset where the goal is to predict the orientations of 3D objects by looking at their 2D images. Our methods outperform the compared methods by a large margin

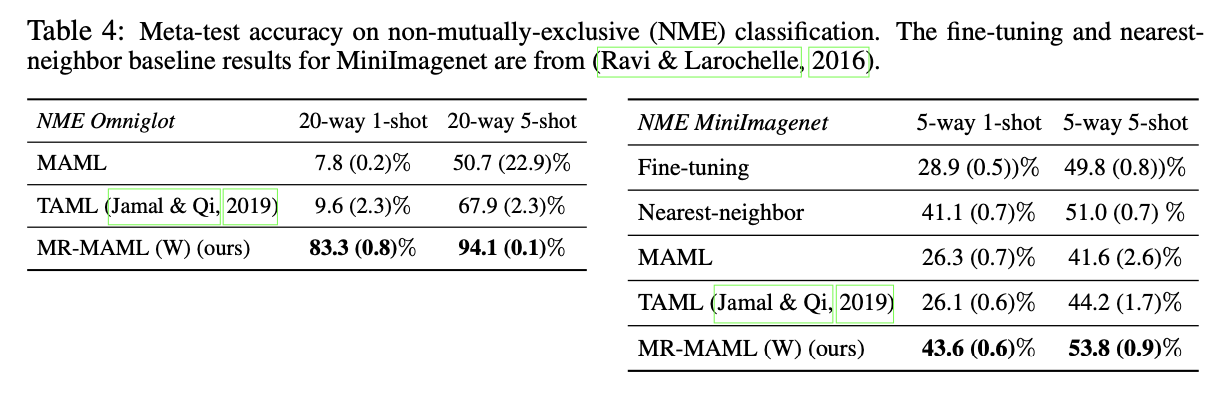
We test on the non-mutually exclusive few-shot classification problems, for which standard meta-learning methods can even give near random predictions in some cases. Our methods provide a remedy.

Takeaways

• Memorization is a prevalent problem in many meta-learning applications and algorithms
• Memorization problem is meta-overfitting at the task level; it differs from standard datapoint-level overfitting. The model can generalize to new points within a training task, but cannot generalize to a new task
• Meta-regularization can effectively control the memorization problem, which expands the meta-learning to the domains that it was once hard to be effective on
• 👉 Keep calm and remain adaptive!

Thanks to the collaborations of Drs. George Tucker, Mingyuan Zhou, Sergey Levine and Chelsea Finn